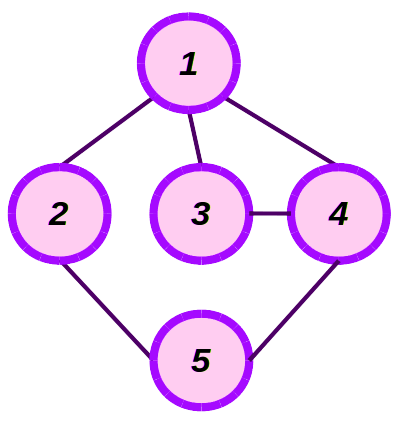
Idiom #129 Breadth-first traversal in a graph
Call the function f on every vertex accessible from the vertex start, in breadth-first prefix order
struct Vertex<V> {
value: V,
neighbours: Vec<Weak<RefCell<Vertex<V>>>>,
}
// ...
fn bft(start: Rc<RefCell<Vertex<V>>>, f: impl Fn(&V)) {
let mut q = vec![start];
let mut i = 0;
while i < q.len() {
let v = Rc::clone(&q[i]);
i += 1;
(f)(&v.borrow().value);
for n in &v.borrow().neighbours {
let n = n.upgrade().expect("Invalid neighbour");
if q.iter().all(|v| v.as_ptr() != n.as_ptr()) {
q.push(n);
}
}
}
}